CS 575 Supercomputing - Lecture Outline
Section III: Shared-Memory Parallel Processors
Chapter 9: Understanding Parallelism
03Nov03 (Week 10)

Dr. Kris Stewart (stewart@rohan.sdsu.edu)
San Diego State University

This URL is http://www.stewart.cs.sdsu.edu/cs575/lecs/ch09.html

Section III of our text will cover:

  1. Ch 9 Understanding Parallelism
  2. Ch 10 Shared-Memory Multiprocessors
  3. Ch 11 Programming Shared-Memory Multiprocessors

Review Class Calendar
Review Class Assignments (with dates now)

You are have looked at a computational experiment involving Linear Algebra and you may find the the following document (which we first examined during Lab 15Sept03):

Forms for HPC Linear Algebra,

useful. This sets up Fine Grain Parallelism using the hardware pipelined architecture found in Vector Supercomputers.

You also just completed working on timing the solution of

Steady-state Heat Diffusion Problem to motivate Ax=b

on the campus Rohan computer, a scalar computer.

Let's use the following sample loops to focus our attention today: 

do i=1,n
   a(i) = x(i) + y(i)
   d(i) = x(i) * f(i)
end do
On a scalar computer, the order of computation would be
a(1), d(1), a(2), d(2), a(3), d(3), and so forth to a(n), d(n)

On a vector computer, the order of computation would be
a(1), a(2), a(3), ..., a(n), then d(1), d(2), d(3), ..., d(n)

Does the ordering make a difference above? [not in this example]. But there are many different computing platforms that have been characterized by Michael Flynn:

Fig. 12.10 Flynn's Taxonomy Michael Flynn's Taxonomy
© O'Reilly Publishers (Used with permission)

Flynn's Taxonomy, a more descriptive diagram from csep1.phy.ornl.gov/gif_figures/caf4.gif

Our goal is to understand the tasks the compiler performs on our behalf when we use the IBM Blue Horizon. The accounts are being created for us now and will be distributed after we have had our class group presentations and discussion on computer security.

Scalable Parallel Architectures and Their Software (especially note slide #34, #41 and #42) from the August 2002 NPACI Workshop. We also will become familiar with NPACI Architectures (especially note slide #3, #9 and #13), from the August 2003 NPACI Workshop at the San Diego Supercomputer Center. The first slides should be somewhat familiar concepts. It is the goal of this course to develop your understanding with the ones.

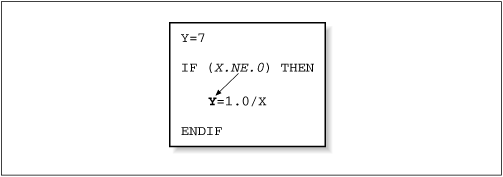
Some sample codes with dependencies

The notation in these diagrams uses the arrow starting at the source of the dependency and ends at the instruction that must be delayed due to the dependency.

Fig. 9-1 Control dependency

© O'Reilly Publishers (Used with permission)

Due to the Control-structure of the If statement, the compiler is unable to predict if the variable Y will be reset by Y = 1.0/X.
Think about this code fragment, is there a better way to avoid a possible divide by zero?

Fig. 9-4 Types of data dependencies

© O'Reilly Publishers (Used with permission)

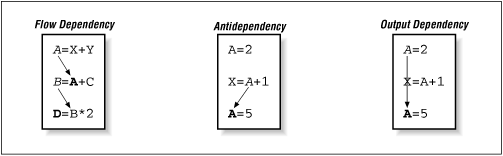
Flow dependencies (or backward dependencies) are defined on p. 183 where our text states they are common in Gaussian elimination. The text provides the example: 

DO I=2,N
	A(I) = A(I-1) + B(I)
END DO
by replicating code, we can reduce the dependency, with an extra addition. 
DO I=2,N,2
	A(I) = A(I-1) + B(I)
	A(I+1) = A(I-1) + B(I) + B(I+1)
END DO
allowing the computation of A(2), A(3) then A(4), A(5), a modest increase in parallelism.

Antidependency is defined on p. 184 with the example below. "You must be sure that the instruction that uses A(I+2) does so before the previous one redefines it." 

DO I=1,N
	A(I) = B(I) * E
	B(I) = A(I+2) * C
END DO
"We can directly unroll the loop and find some parallelism:"
  1. A(I) = B(I) * E
  2. B(I) = A(I+2) * C
  3. A(I+1) = B(I+1) * E
  4. B(I+1) = A(I+3) * C

  5. A(I+2) = B(I+2) * E
  6. B(I+2) = A(I+4) * C
  7. A(I+3) = B(I+2) * E
  8. B(I+3) = A(I+5) * C
"Statements 1-4 could all be executed simultaneously. Once those statements complete, statments 5-8 could execute in parallel."
** NOTE ** our text has a typo - it has no statements 7 and 8.

Output dependency is defined on p. 185 as "getting the right values to the right variables when all the calculations have been completed."

Dependencies Within an Iteration 

DO I=1,N
   D = B(I) * 17
   A(I) = D + 14
ENDDO
The variable D has a flow dependency and delays the execution of the second statement in the loop. This will limit parallelism and closer examination, manually unrolling the loop several times shows 
D = B(I) * 17
A(I) = D + 14
D = B(I+1) * 17
A(I+1) = D + 14
D = B(I+2) * 17
A(I+2) = D + 14
revealing the variable D has flow, output and antidependencies. The technique to ensure parallelization, at the cost of some memory, is to promote the scalar to a vector 
DO I = 1,N
   D(I) = B(I) * 17
   A(I) = D(I) + 14
ENDDO

Some additional examples not covered in our text, 

DO I=1,N
	C(I) = D(I) * C(INDEX(I))
END DO
The compiler cannot determine if C(INDEX(I)) is a recurrence, so this won't be vectorized. Note: Suppose the programmer knows that the INDEX will not bring in an recurrence. The programmer can share this knowledge with the compiler through a compiler directive: 
$IVDEP
DO I=1,N
	C(INDEX(I)) = D(I) * B(INDEX(I))
END DO

Loop Splitting 

DO I=1,N
	A(I) = X(I) + Y(I) + INTERP(X(I))
	B(I) = SIN(X(I)) + Z(I)
END DO

This loop cannot be vectorized due to the subprogram all INTERP. But, if we split the loop, 

DO I=1,N
	A(I) = X(I) + Y(I) + INTERP(X(I))
END DO
DO I=1,N
	B(I) = SIN(X(I)) + Z(I)
END DO
Now the first loop still does not vectorize, but the second one is a vector loop.

Loop Fusing Consider two loops with similar ranges of indices: 

DO I=1,N
	A(I) = X(I) + Y(I)
END DO
DO I=1,N-1
	B(I) = X(I) + Z(I)
END DO
We can reduce loop overhead and memory references compared to the number of floating point operations by 
DO I=1,N-1
	A(I) = X(I) + Y(I)
	B(I) = X(I) + Z(I)
END DO
A(N) = X(N) + Y(N)
Here is the reality of programming. You may have multiple depedencies in a single fragment of code.

Fig. 9-5 Multiple dependencies

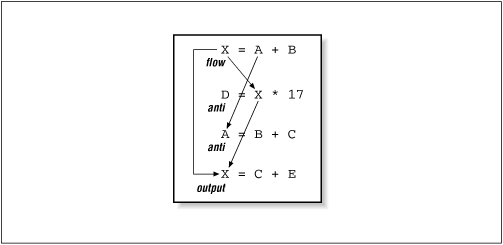
© O'Reilly Publishers (Used with permission)

If you were taking CS 524 Compiler Construction, we would study the representations presented in this chapter in Figures 9-6, 9-7, 9-8, 9-9, 9-10. But just as this is not a class in numerical analysis, it is also not a class in compiler construction, so I'll omit them.
Return to CS 575 Class Page