- First instruction mix example (p. 148)
-
DO I=1,N A(I,J,K) = A(I,J,K) + B(J,I,K) ENDDO
One floating point operation and three memory references (2 loads; 1 store). 3:1 ratio of memory reference to floating point operations means we expect no more than 1/3 peak floating point performance, unless we have more than one path to memory. Bad news for performance, but good information to know. - Second instruction mix example (p. 148)
-
DO I=1,N A(I) = A(I) + B(J) ENDDO
One floating point operation and two memory operations (1 load; 1 store). 2:1 ratio memrefs to floating point. Compiler should be smart enough to notice that B(J) is loop-invariant and load it only once.
Now consider the C code to multiply two vectors of complex numbers xi = (x_ri,x_ii) for the real and imaginary part of the number.
for (i=0; i < n; i++) {
xr[i] = xr[i]*yr[i] - xi[i]*yi[i];
xi[i] = xr[i]*yi[i] + xi[i]*yr[i];
}
We now have 6 memory references (4 loads, 2 stores) and 6 floating
point operations (2 adds and 4 multiplies)
How would you see the effective of any detailed analysis? You would examine the generated assembler code, which for the Sun architecture is handled nicely.
f90 -S sgefa.f
sgefa.s compiler-generated RISC assembly code.Notice in this RISC assembly code what is generated at source line 59 for the DO loop at line 60.
Fig. 8-1 Arrays A and B
© O'Reilly Publishers (Used with permission)
But these 2D arrangements of data are linearized for storage in the computer. (Fortran stores by columns; C stores by row)
DO I=1,N DO J=1,N A(J,I) = A(J,I) + B(I,J) ENDDO ENDDOOne array is referenced with unit stride, the other with a stride of N.
Fig. 8-2 How array elements are stored Note: the cache line boundary. The array A references elements
likely to still be within a cache, but array B references elements in
separate columns, therefore in separate cache loads (illustrated in
the top image of Fig. 8.3.
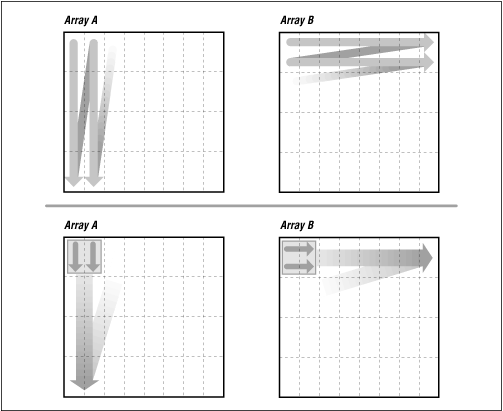
Loop-unrolling of the inner and outer loop can help:
We help the compiler out by rearranging loops to work with small
2 by 2 squares of the portion of array A and array B, as in the bottom
image of Fig. 8.3, by unrolling our own loops to ensure the TLB (translation
look-ahead buffer), a cache of precomputed array element locations, will
have the address of memory data needed. We cut the original loop in
two parts to save TLB entries.
Fig. 8-3 2x2 squares (loop-unrolling)
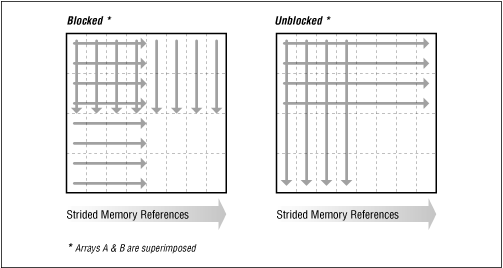
We can take this even further by rewriting the inner loop to take advantage
of block data, illustrated below in Fig. 8-4.
Fig. 8-4 Picture of unblocked versus blocked references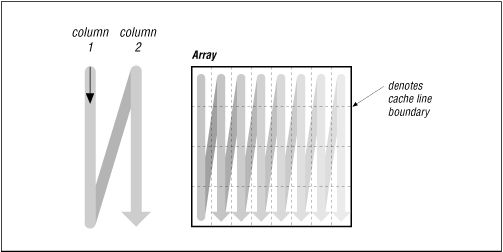
© O'Reilly Publishers (Used with permission)
DO I=1,N,2
DO J=1,N,2
A(J,I) = A(J,I) + B(I,J)
A(J+1,I) = A(J+1,I) + B(I,J+1)
A(J,I+1) = A(J,I+1) + B(I+1,J)
A(J+1,I+1) = A(J+1,I+1) + B(I+1,J+1)
ENDDO
ENDDO
© O'Reilly Publishers
(Used with permission)
DO I=1,N,2
DO J=1,N/2,2
A(J,I) = A(J,I) + B(I,J)
A(J+1,I) = A(J+1,I) + B(I+1,J)
A(J,I+1) = A(J,I+1) + B(I+1,J)
A(J+1,I) = A(J+1,I) + B(I+1,J)
ENDDO
ENDDO
DO I=1,N,2
DO J=N/2+1,N,2
A(J,I) = A(J,I) + B(I,J)
A(J+1,I) = A(J+1,I) + B(I+1,J)
A(J,I+1) = A(J,I+1) + B(I+1,J)
A(J+1,I+1) = A(J+1,I+1) + B(I+1,J+1)
ENDDO
ENDDO
© O'Reilly Publishers
(Used with permission)
Return to CS 575 home page