CS 575 Supercomputing - Lecture Outline
Chapter 5: What a Compiler Does - Outline
October 6, 2003
This URL is http://www.stewart.cs.sdsu.edu/cs575/lecs/ch05.html
An review from last Wednesday's lab using the compiler flags
Lab 3 Floating Point and
Compiler Flags
Since the sample code used generates a long listing of computed output
values, followed at the end by a run-time, how would you compare
the similarity of this vector of output?
Ans: Subtract the corresponding vector components and then find
the largest absolute value, along with the vector index of where it occurs.
This is called a Vector Norm.
But, why?
Ans: This measures the size of a vector.
Compiler translates source code in a High Level Language (HLL) to the native machine code for the platform you are using.
- cc man page
- cc -flags page
- Fortran 90 man page [or
%f95 -xhelp=readme from Xwindows command line (%)]
- f90 -flags page
One of the goals of this class is for you to develop the understanding of
performance issues to see the usefulness, value and ways to effectively
use these programming tools.
Would CS 107 care more about compile time or run time?
What does the compiler do to try to optimize your code? (Text: Ch. 5)
- Copy Propagation
- Constant Folding
- Dead Code Removal
- Strength Reduction
- Common Subexpression Elimination
- Loop Invariant Code Motion
- Induction Variable Simplification
- Scalar Optimizations even Rohan does
Fig. 5-1 Basic compiler processes
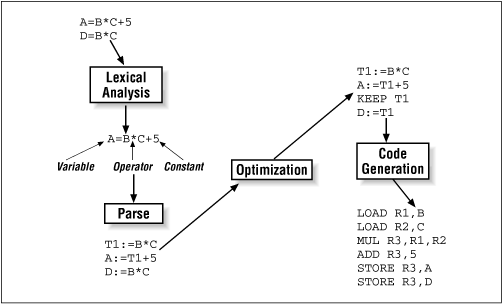
© O'Reilly Publishers (Used with permission)
NOTE: typo in Fig. 5-1 in the Code Generation portion
LOAD R1,B
LOAD R2,C
MUL R3,R1,R2
STORE R3,D <-- must store the results of B * C
ADD R3,5 <-- now can update B * C + 5
STORE R3,A
Our text uses the sample code
A = -B + C * D / E
to motivate the discussion of Intermediate Language Representation,
where Temporary Variables (T) are used, representing values to be
kept in registers, perhaps. Our text rules for Intermediate Language
Representation (p. 87):
"Rules for Intermediate Lanuage Representation"
- Instructions consists of one opcode, two operands and a result. Operands may be empty.
- Assignments are of the form: X := Y op Z, meaning X gets the
result of op applied to Y and Z
- All memory references are explicit load from or store to
"temporaries" T#
- Logical values used in branches are calculated separately from the
actual branch.
- Jumps go to absolute addresses.
T1 = D / E
T2 = C * T1
T3 = -B
A = T3 + T2
Recall: This is not a course in Compiler Construction. We want
to develop some familiarity with the level the compiler works at to
highlight the possible optimizations.
An even more detailed example is developed for a loop structure
while (j < n) {
k = k + j * 2;
m = j * 2;
j++;
}
Translated into Intermediate Language Representation:
A:: t1 := j
t2 := n
t3 := t1 < t2
jmp (B) t3
jmp (C) TRUE
B:: t4 := k
t5 := j
t6 := t5 * 2
t7 := t4 + t6
k := t7
t8 := j
t9 := t8 * 2
m := t9
t10:= j
t11:= t10 + 1
j := t11
jmp (A) TRUE
C::
Fig. 5-2 Intermediate language divided into basic blocks
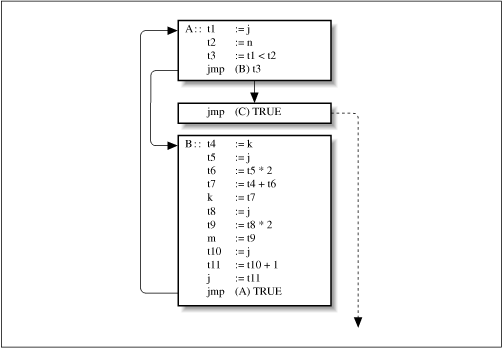
© O'Reilly Publishers
(Used with permission)
Have you had a chance to use the SUN WorkShop?
This
programming environment supports both C and Fortran 90.
Today we will start with pointing to some sample codes that can be used
to generate examples of using the optimization properties of the
Fortran 90 compiler. In a later lecture, we will examine this for
C programs.
SUN WorkShop man page
You can access a wealth of information on the SUN WorkShop (Forte Developer 6
update 2) when logged onto a Rohan account, starting a web browser,
entering the url
file:/opt/SUNWspro/docs/index.html/
Why do you have to log onto your Rohan account first?
Explorations from the command line:
- Begin by obtaining your own copy of the example-suite slinpack
- cp -r /opt/SUNWspro/examples/WorkShop/slinpack .
We use this LINPACK routine since it is part of the
benchmarking suite
that determines the Top 500 High Performance Computing platforms:
Top 500
Where is the San Diego Supercomputer Center (SDSC)'s Blue Horizon?
Ans: #13 in the World!
- Experiment with the time to compile the routine
- f90 slinpack.f -time -o slinpack_f90
- slinpack_f90
- f90 slinpack.f -time -O2 -o slinpack_f90_o2
- slinpack_f90_o2
- Source Code for Slinpack
- Recall our previous exploration of the timing evidence for the
expected amount of work in a program. You may recall that Gaussian
Elimination for the linear system, Ax = b, when the matrix A is N by N,
uses 2 N3 / 3 operations (adds and multiplies) as
the high order measure of Work. What do we expect the cost to be
when the size of the matrix A doubles?
Work(N) ~ 2 N3 / 3
Work(2N) ~ 2 [2N]3 / 3 = 8 * 2 N3 / 3 = 8 * Work(N)
Work(2N) / Work(N) ~ 8
is our expectation.
Will we be able to verify this through a computational experiment?
We will continue this discussion on Wednesday as we set up the second
computational experiment. Due date: 29Oct03
Examine
the increased time to compile in a "multipass" way to provide
optimized code
the enhanced (smaller) execution time in the output when -O2 is used
Back to CS 575 Supercomputing home page


