CS 575 Supercomputing - Lecture Outline
Chapter 4: Floating-Point Numbers - 29 Sept 2003

Dr. Kris Stewart (stewart@sdsu.edu)
San Diego State University

This URL is stewart.sdsu.edu/cs575/lecs/ch04.html

Reality and Representation

"The world is full of real numbers." For example, pi = 4.0 * atan(1.0) = 3.14159 26535 89793 ... a non-terminating decimal value. Other values you are familiar with such as 1/10, also may have a difficulty in being represented exactly in a digital world. What is 0.1 in as a binary fraction? That is, as a quantity that can be represented by a computer exactly?
(0.1)₁₀ = (0.000110...)₂ (see below)

What about the ruler? The one I have brought to class today can measure up to a magnitude of 12 inches with a precision of 1/16 inch. What do you do if the item you are measuring does not fall exactly on one of the pre-printed marks?

Rational Numbers (Fractions) Fig. 4-1 Rational number mathematics

© O'Reilly Publishers (Used with permission)

Symbolic mathematical packages, such as maple and mathematica provide the capability to exactly represent values such as these - at the cost of storing each digit in the numerator and the denominator and performing any needed arithmetic by using the greatest common divisor (GCD) to reduce fractions to their simplest form. Even with the growing speed of CPUs, the cost can be prohibitive when millions of arithmetic operations need to be performed in scientific simulations.

Fixed Point

Banks need to maintain representation of numbers to the penny, therefore given the range in this situation is known, the values can be stored in fixed point as scaled integers, e.g. 110.77 scaled by 100 would be stored as 11077. But what about interest calculations? $125.87 at 4% interest should earn you $5.0348 in a year. If your bank only has two digits of accuracy, as above with scaling by 100, someone keeps the $0.0048 - does your bank round or truncate?

Mantissa/Exponent

The floating-point format most prevalent in HPC is based on scientific notation, using a

• mantissa,
• base and
• exponent,

e.g. 6.02 * 10^23. NOTE: once the engineer who designs the hardware chooses how many digits to store, these are all integer valued quantities, which can be exactly represented, as done for fixed-point numbers before. This provides a wide coverage from the infinitely large possible set of reals. This is needed because different fields of science and engineering have different needs:

• Biologists who study population dynamics need to be able to represent, for example, 270 Million people, but a half person does not make sense. Other biologists may study organisms on the microscopic scale in their molecular studies.
• Astronomers measure distances between galaxies which are very large magnitude values.
• Other disciplines and their scales that the class is familiar with?

Fig. 4-2 Distance between successive floating-point numbers

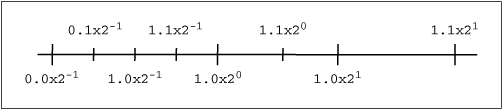
© O'Reilly Publishers (Used with permission)

You can have multiple presentations of the same value:
6.00 * 10^5 = 0.60 * 10^6 = 0.06 * 10^7 = 600,000 = six hundred thousand
therefore, by convention, shift the mantissa (and adjust the exponent) until there is exactly one nonzero digits to the left of the decimal point (called normalized), therefore use 6.0*10^5 or 6.0E5 since the base of 10 can be assumed..

Fig. 4-3 Normalized floating-point numbers

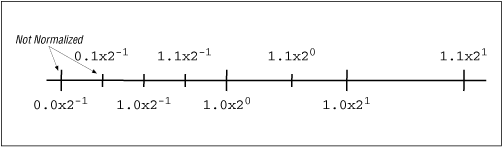
© O'Reilly Publishers (Used with permission)

There is a loss of precision. 1/2 and 0.25 can be represented exactly as binary fractions. Can you give them?

But 1/10 = 0.1 cannot be represented exactly as a binary fraction. Wednesday's Lab (1Oct03), we will briefly examine Exercise 1 (p. 77) from this chapter to see that adding 1/10 to itself 10 times does not yield 1.

---

NOTE:

• 0.5₁₀ = 0.1₂,
• 0.25₁₀ = 0.01₂,
• 0.1₁₀ = 0.00011001...₂

---

More Algebra that Doesn't work

Consider the code fragment performed with REAL*4 variables, which typically have 7 digits of precision:

X = 1.25E8
Y = X + 7.5E-3
IF (X .EQ. Y) THEN
   PRINT*, "Am I nuts or what?"
ENDIF

Fig. 4-4 Loss of accuracy while aligning decimal points

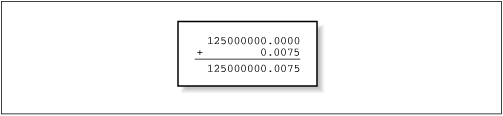
© O'Reilly Publishers (Used with permission)

The .0075 part in the result will be dropped off (truncated or rounded) when this value is stored to memory.

Another facet is that mathematical properties, such as addition is commutative and associative will not hold true.

(X + Y) + Z = (Y + X) + Z - commutative is okay
(X + Y) + Z = X + (Y + Z) - associative does NOT hold

And our text provides the following example. Assume our computer can perform arithmetic with only five significant digits and let X = .00005, Y = .00005, and Z = 1.0000

(X + Y) + Z = .00005 + .00005 + 1.0000
            =     .00010      + 1.0000 = 1.0001
X + (Y + Z) = .00005 + .00005 + 1.0000
            = .00005 +     1.0000      = 1.0000

Whenever possible, add the small numbers together first.

Improving Accuracy Using Guard Digits

Fig. 4-5 Need for guard digits (example of a subtraction)

© O'Reilly Publishers

Formatting (by programmer source code)

When the user program outputs a value, the amount of information printed to the print or to the screen is determined by a specific format statement or by the language default. For floating point numbers, the C language uses the %8.2f as the default format, for example in a fprintf or print* statement.

C Language Format Conversion specification strings

Fortran Formats

What happens if the programmer specifies a format and the computed value is represented as 0.0?

What if a value is computed that is too large to fit in the computer word?

Overflow

What if a value is computed that is too small to fit in the computer word?

Underflow

Harmonic Series converges in computer arithmetic

A famous example from your calculus course is the harmonic series,
SUM_i=1^inf 1/i
1 + 1/2 + 1/3 + 1/4 + 1/5 + 1/6 + = ?
which mathematics tells us will not converge to a value. But what happens if you sum this series on a computer using floating-point numbers? Think about, what if you summed it backwards? Pick a value of N and add up
1 + 1/2 + 1/3 + ... + 1/N
You can make a table of N and Harmonic Series(N)

IEEE Floating-Point Standard

During the 1980's, the Institute for Electrical and Elecronics Engineers (IEEE) produced a standard for the float-point format, strongly led by W.B. Kahan, UC Berkeley, the IEEE 754 floating-point format. An Interview with the Old Man of Floating-Point Reminiscences elicited from William Kahan by Charles Severance. The efforts by many to produce a standard that has been adopted by nearly all computer manufacturers today has greatly simplified the life of the HPC programmer.

In the diagram below, the field exp determines the magnitude (size) of the numbers that can be presentated. The field mantissa determines the precision (accuracy) that the number has. The one-bit field s determines the sign of the number (+ or -).

Fig. 4-6 IEEE 754 floating-point formats

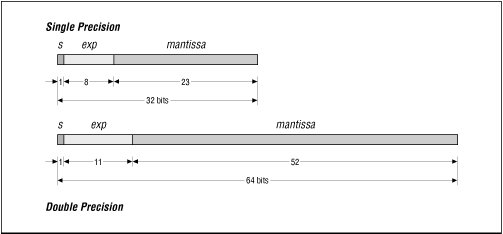
© O'Reilly Publishers Used with permission)

IEEE 754 Floating-Point Format

This widely-debated and now adopted format specifies

1. Storage format
2. Precise specifications of the results of operations
3. Special values
4. Specified runtime behavior on illegal operations

We will be using well-designed mathematical software in this course, so most of the "concerns" regarding floating point behavior described in this chapter are taken can of - except for your "drivers" (main programs).

This is not a course in Numerical Analysis, nor a course in Compiler Construction nor Computer Design. We will be using good software and and a very well engineeering computing platform, so your goal is to learn to quantify how good they are.

In lab on Wednesday (1Oct03), you will examine the source code from our textbook (p. 77) textp77.f along with some other examples to prepare you for the Second Computational Experiment and Report.

PROGRAM C8_ex04
!
! Examples of the use of the kind function and the numeric inquiry functions
!
! Integer arithmetic
! ------------------
!
! 32 bits is a common word size, and this leads quite cleanly to the following
!
! 8 bit integers       -128   to        127       or  10**2
! 16 bit integers    -32768   to       32767      or  10**4
! 32 bit integers -2147483648 to   2147483647     or  10**9
!
!
IMPLICIT NONE
INTEGER                                :: I
INTEGER ( SELECTED_INT_KIND( 2))       :: I1
INTEGER ( SELECTED_INT_KIND( 4))       :: I2
INTEGER ( SELECTED_INT_KIND( 9))       :: I3
! Real arithmetic
! ---------------
! 32 bits is a common word size, but 64 bits is also available
!
! 32 bit integers 8 bit exponent, 24 bit mantissa
! This applies on both DEC VAX and the Intel family
! of processors, i.e. 80386, 80486.
!
! 64 bits. Two choices here, simply double the precision
! and keep the mantissa the same or alter both.
!
! 64 bit  8/56 exponent/mantissa - same as for 32 bit
! 64 bit 11/53 exponent/mantissa - now have approximately the same
! precision as for 56 bit mantissa, but the range is now ~ 10**308
! much more useful in the scientific world.

rohan.stewart:~/cs575/fall03/testmachine> link -c08
 
  Integer values
  Kind    Huge
 
   4   2147483647
 
   1   127
   2   32767
   4   2147483647
 
  Real values
  Kind    Huge              Precision       epsilon
 
 
   4   3.4028234E+38             6   1.1920929E-7
   8   1.7976931348623157E+308   15   2.220446049250313E-16

Return to CS 575 Supercomputing - Class home page